A Floating Point Joke
Next time you hear that “there are 10 types of people in the world, those who understand binary and those who don't”, remember that:
There are roughly 0011111111111111 types of people in the world, those who understand floating point numbers, and those who don't.
It's possible that you don't get it – when those 16 bits are interpreted by a computer as a real number, they mean “very nearly two”. You may laugh now.
An explanation
The 16 bits are interpreted in three sections, summarised in the table below, and the final value (“very nearly two”) is the product of all three.
| Bits | Name | Value |
|---|---|---|
0............... |
Sign | positive |
.01111.......... |
Exponent | $$2^{(15-15)} = 1$$ |
......1111111111 |
Fraction | 1.999023 |
The sign
The first bit is the sign and 0 means positive.
The exponent
The exponent determines the order of magnitude of the represented number. The five bits 01111 are interpreted as base 2 (binary as in the “10 types of people” joke), which comes to $1+2+4+8=15$.
That value is used as $n$ to calculate $2^{(n-15)}$, and was deliberately chosen here so that the exponent is $2^0 = 1$. The -15 is known as the “zero offset”.
The fraction
The remaining bits each represent a value in the series $2^{-n}$. If set, the first bit has value $\frac{1}{2}$ and every other bit is worth half of the previous one. The fractional part of the floating point number (also called the mantissa) is the sum of those values, plus one. It may help you remember that additional one if you think of it as an implied leading bit, or it may not. The effect is that the fraction is always between 1 and very nearly 2.
The fraction therefore has the value
$1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256} + \frac{1}{512} + \frac{1}{1024} =$1.999023
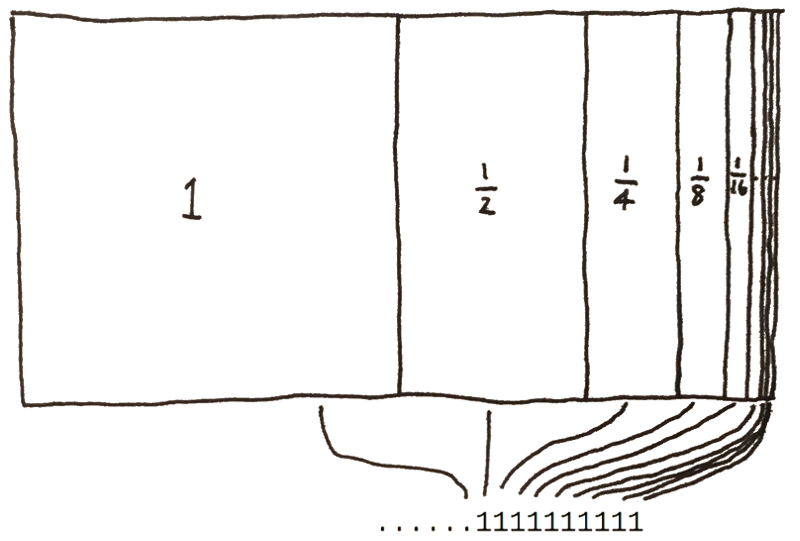
The first “1” is implied and each subsequent bit halves in value. The sum is almost two.
The punchline
Putting it all together produces $(+1 \times 1 \times 1.999023) = 1.999023$
It doesn't quite split people into two categories. It means that there are roughly 1.999023 types of people in the world, and not one of them should expect perfect representations of real numbers from floating point approximations.
Meanwhile, in the real world
All of the above is for a 16-bit floating point number, known as “half-precision”, but 32 or 64 bits are more common. They are interpreted in the same way, but with different sizes of exponents, fractions and zero offsets - for details, see IEEE754. If you make the leading two bits 0 and the remainder 1, then the longer the representation, the closer it can get to 2. For example with 32 bits 00111111111111111111111111111111 is 1.999998.
Unlike most real numbers, there are exact representations of decimal 2 in this format, for example 0100000000000000, an exponent of 21 multiplied by a mantissa of all zeros (remember the implied leading bit of 1, so a mantissa of zeros multiplies the exponent by 1). But where's the fun in that?
⁂